Tout commence au 3e siècle avant notre ère. Cela fait déjà quelque temps que l’on suppose que la Terre est ronde comme un ballon, plutôt que plate comme une pizza (qui n’existe pas encore à l’époque, de toute façon). Mais allez prouver ça ! Eh bien Ératosthène, il l’a fait, en se servant juste de ses yeux, d’un puits et d’un bâton.
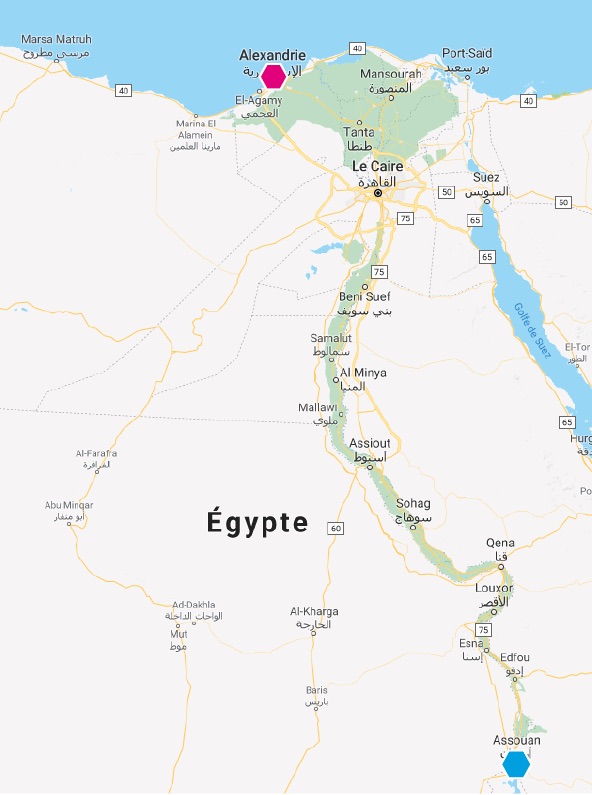
À l’époque, Eratosthène dirige la fameuse bibliothèque d’Alexandrie, au nord de l’Égypte. Il apprend que dans la ville de Syène, aujourd’hui appelée Assouan, tout à fait au sud du pays, le soleil éclaire le fond des puits à midi pile le 21 juin, date du solstice d’été (le moment de l’année où le Soleil est le plus haut dans le ciel, et où la journée est la plus longue). Il n’y a aucune ombre à l’intérieur, et si on plante un bâton au fond, il ne projette pas d’ombre non plus. Ce qui signifie que le soleil est pile à la verticale.
Fais l’essai avec une lampe de poche et un tube en carton posé droit sur une table : si tu mets la lumière pile au-dessus du trou, elle éclaire la table au fond du tube, mais si tu la décales de n’importe quel côté, il y a une ombre !
Bref. Ératosthène réfléchit et se dit que le Soleil, qui est super loin, doit envoyer des rayons parallèles entre eux sur toute la Terre. Donc, si la Terre était plate, on devrait observer le même phénomène au solstice d’été loin au nord ou au sud de Syène, disons par exemple… à Alexandrie, qui se trouve à plus de 1 000 km au nord. Mais si la surface de la Terre est bien courbe, alors un bâton planté verticalement à Alexandrie devrait au contraire projeter une ombre.
C’est plus clair avec ce schéma :
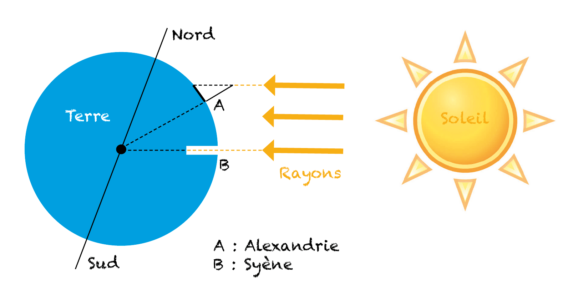
Au solstice d’été suivant, Eratosthène fait l’expérience en plantant un gnomon (sorte de bâton) bien droit dans le sol à Alexandrie. Bingo : il observe une ombre projetée au pied du bâton en plein midi !
Conclusion : oui, la Terre est bien ronde, comme d’autres observations en avaient donné l’intuition aux philosophes grecs (voir le récit dans ton magazine Curionautes des sciences n°1).
Mais Ératosthène ne s’arrête pas là : il va carrément calculer, avec une grande précision pour l’époque, combien mesure le tour de la Terre. Tout ça à partir de la fameuse ombre mesurée au pied du gnomon, de la distance approximative entre Syène et Alexandrie, et de notions de géométrie niveau collège ! Mais ça, c’est une autre histoire…